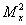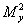M²-Sensor for the Adaptive Optical System
Abstract
When adaptive optical system is applied for laser beam control it is very important to
know the beam parameters such as beam width, divergence angle, beam quality factor M2 etc.
before and after correction. That is why the sensor making such estimations should be included in any laser
adaptive optical system. This paper describes the sensor design, possibilities, the principals of measurements
and it’s place in the whole adaptive optical system.
Keywords: beam widths, beam quality factor M2, adaptive system.
Introduction
A good laser beam quality is necessary for many scientific and industrial applications for
example for material processing. Different active medium inhomogeneities and turbulence of the air at the beam
delivery path cause laser beam phase and intensity distortions and power instability. To improve laser beam
parameters adaptive optical system could be used.
In our group of Adaptive Optics for Industry and Medicine, ILIT, Russian Academy of Sciences we
design and make commercially available adaptive optical system for correction of the wavefront aberrations and for
formation of a specified laser beam intensity distribution. The main element of our adaptive system is a bimorph
flexible mirror well described in Ref.1-5. For the wavefront analysis we use the Shack-Hartmann sensor. For the
estimations of laser beam widths, divergence angle, beam quality factor M2, power instability we designed
so-called M2-Sensor. The place of the M2-Sensor in the whole adaptive system
infrastructure is shown in Fig.1.
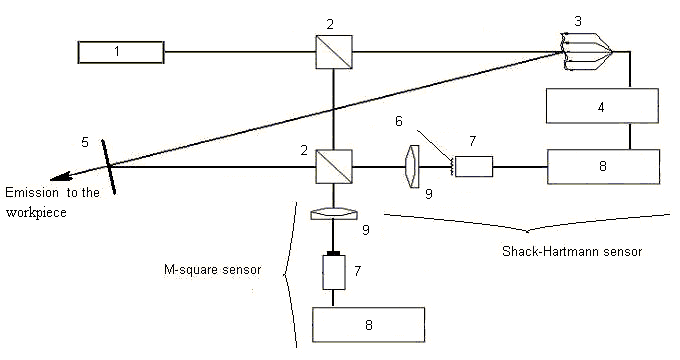
Fig.1. Adaptive system with the M²-Sensor: 1 – laser; 2 – beam splitter, 3 – deformable mirror,
4 – mirror control unit, 5 – semi transparent mirror, 6 – lenslet array, 7 – CCD camera, 8 – computer, 9 – focusing lens
Methods and equiations for beam parameters calculation
According to the International standard ISO11146 different methods of beam parameters
determination could be applied6-10. In our case we use the direct method of beam parameters measurement.
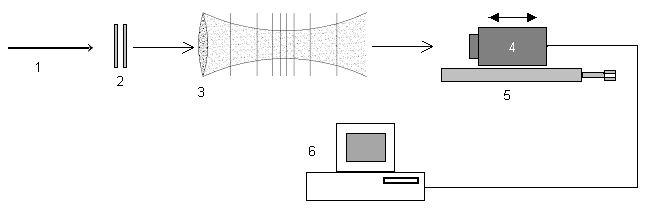
The more detailed scheme of the M²-Sensor and it’s photo are presented in Fig.2.
(a)
 (b)
(b)

Fig.2. M²-Sensor design: 1 –laser beam, 2 – neutral density variable filter, 3 – focusing lens, 4 – CCD camera, 5 – moving stage, 6 – computer with framegrabber , (b) The photo of M²-Sensor
To estimate divergence angle, beam quality factor M2 the beam diameter value is
used 6. In order to calculate beam diameter intensity distribution is registered with the CCD. The beam
diameters along x and y directions are defined as:
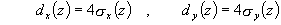 , (1)
, (1)
where the second moments σx, σy of the intensity distribution
I(x,y,z) at the location z are given by:
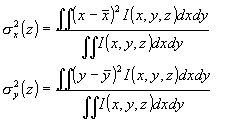 , (2)
, (2)
Here 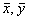 are the first moments of the intensity distribution
giving coordinates of the beam centre:
are the first moments of the intensity distribution
giving coordinates of the beam centre:
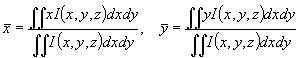 . (3)
. (3)
For elliptical beams the software includes the calculation of the azimuthal angle
φ between the beam principal axes x', y' and the axis of laboratory coordinate system x, y (Fig.3).
Then the definition of all the main beam parameters takes place in the principal beams axis direction.
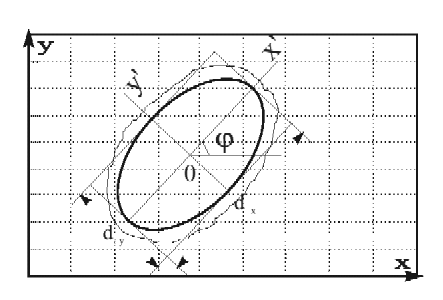
Fig.3. Elliptical beam
In order to reduce an influence of different expose signals it is possible to select an area of
interest for calculations from the whole surface of the CCD window (Fig.4). To increase the accuracy of calculations
the dark current of camera is subtracted from the image.
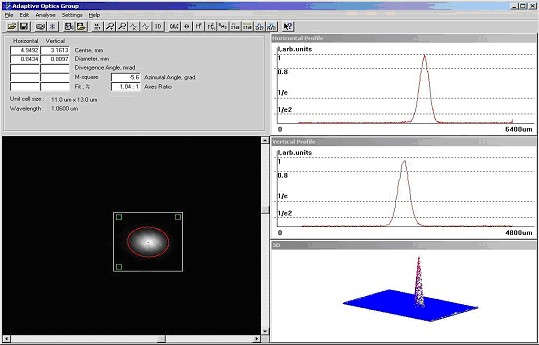
Fig.4. Selecting of an area of interest
Our sensor allows to define the beam quality factor M2 and divergence angle by two
methods described in ISO11146 6.
The first one is based on a multiple measurements of laser beam diameters in several
cross-sections before and after the beam waist. At least 10 measurements have to be taken - half of them
within one Rayleigh length on either side of the beam waist. The rest measurements have to be taken beyond
double Rayleigh distance on either side of the beam waist. If the beam waist is accessible for direct measurements
the beam parameters are determined by a hyperbolic fit to the measured beam diameters di along
the beam propagation axis:
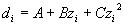 , (4)
, (4)
where di is a beam diameter at the location zi,
A,B,C are the hyperbola parameters. Then the divergence angle and beam propagation factor can be
calculated using:
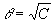 , (5)
, (5)
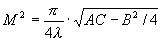 . (6)
. (6)
If the beam waist is not accessible for direct measurements the artificial waist should be
created with the help of a focusing element and then the same measurements should be made around the artificial
beam waist (fig.2).
Fig.5 shows the realization of multiple measurements method by the software of our M2-Sensor.
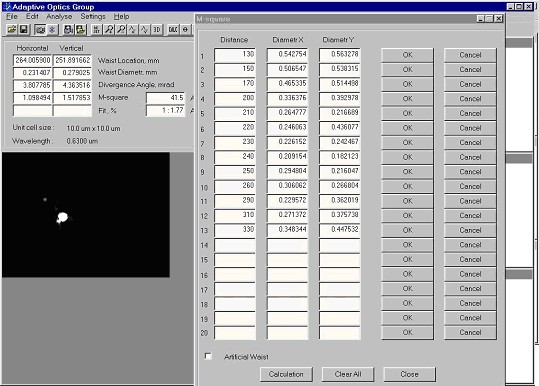
Fig.5. Realization of multiple measurements for determination M2-parameter
The second method to define beam parameters is so-called single measurement method. To use this
method first of all the near-field laser beam diameter d0 is determined. Then the far-field
diameter of the beam d is measured in the focal plane of the lens. M2-factor is calculated according to the formula:
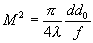 , (7)
, (7)
where f is a focal length of the lens. The divergence angle is determined using the relationship:
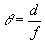 . (8)
. (8)
Gaussian and flat-top fit and oscilloscope options of M2-Sensor
For laser applications sometimes it is useful to know gaussian or flat-top fit to laser beam
intensity. For example, the last one is important during formation of the super-gaussian intensity distribution.
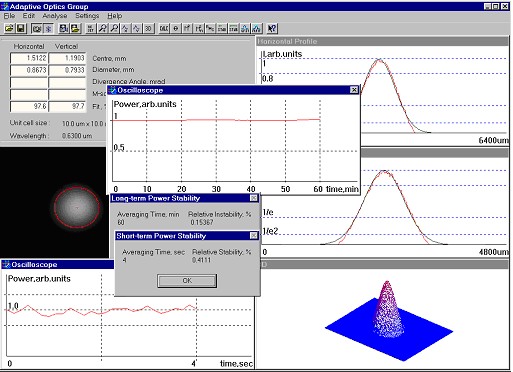
Fig.6. Gaussian fit to the beam intensity and option of oscilloscope
To compare real intensity distribution with gaussian one the following formula is used:
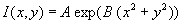 , (9)
, (9)
where I(x,y) is the intensity value of the point with transversal coordinates
(x,y), A,B are coefficients of gaussian function. Then the RMS error σ² is analysed:
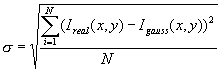 . (10)
. (10)
Here Ireal(x,y) is the real intensity value, Igauss(x,y) is
the calculated gaussian one, N is the number of pairs (x,y) used in fitting. If σ=0 then our
beam becomes the gaussian. The more σ, the less the real intensity distribution function could be described by gaussian function.
While forming super-gaussian intensity distribution in some area (x,y)≤(x0,y0) it
is convenient to use for fitting rectangular function:
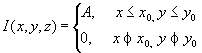 , (11)
, (11)
We minimize the RMS-error of deviation of power of real beam (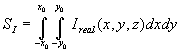 ) and
flat-top one (
) and
flat-top one (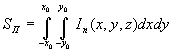 ):
):
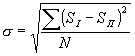 . (12)
. (12)
In order to be sure that during the experiments of the formation of the laser intensity
distribution the important parameters of a laser beam remains as good as before correction the software includes
options for evaluation of the short-term and long-term power stability. The short-term stability defined as:
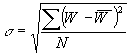 , (13)
, (13)
where W is the power distribution in one frame, 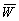 is the averaged power of all frames measured per short time, N is the number of frames.
is the averaged power of all frames measured per short time, N is the number of frames.
The long-term power stability of a laser beam defined as:
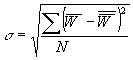 , (14)
, (14)
Here 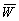 is the short-term averaged power measured for a few
seconds,
is the short-term averaged power measured for a few
seconds, 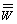 is the averaged one measured for the compatible long time, N is
the number of counts of
is the averaged one measured for the compatible long time, N is
the number of counts of 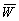 .
.
Fig.6 illustrates the oscilloscope option of M2-Sensor. The frequency of the measurements is 10 Hz.
Accuracy of the measurements
Let’s consider reasons and corresponding errors influenced on the accuracy of measurements. The main reasons are:
- finite CCD resolution - σ1;
- error of CCD position measurements - σ2;
- dark current of the CCD - σ3;
- laser intensity instability - σ4.
So the whole error is:
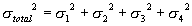 . (15)
. (15)
Estimations shows that in our case:
σ1=0.7%,
σ2≈0,
σ3=6%.
Error caused by laser intensity instability depends on the own laser characteristic. For example
for LGN-302 He-Ne laser this error is σ4=0.01%.
So the total RMS-error is:
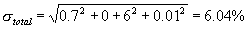 .
.
According to International Standard ISO11146 the admissible mistake for beam parameters
calculation is σtotal=10%.
Two He-Ne lasers were taken for testing of the M2-Sensor: LGN-302 and
LGN-207А. The obtained results are presented in Table 1. All parameters were determined along x and y laser beam directions.
| Parameter
| 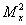
| 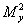
| θx, mrad
| θy, mrad
| σlong-term, %
| σshort-term, %
|
| LGN-302
| 1.17
| 1.36
| 1.116
| 1.044
| 0.01
| 0.2
|
| LGN-207A
| 2.06
| 1.59
| 2.07
| 1.6
| 0.15
| 0.4
|
Table 1. Main results
Conclusion
Our M2-Sensor is designed as a part of adaptive system for simple measurements
of laser beam parameters. The software and hardware allow to define such laser beam characteristics as:
- Beam Centroid location;
- Beam Diameter or Widths;
- Divergence Angle;
- Beam Quality Factor M2;
- Elliptisity of the beam;
- Gaussian and Flat-top fit to the intensity;
- Short-term and Long-term stability of the beam intensity.
All the measurements correspond to the International Standard ISO11146.
References
- A.V. Kudryashov, V.V. Samarkin, “Control of high power CO2 laser beam by adaptive optical elements”, Optics Communications 118, pp.317-322, 1995.
- T.Yu. Cherezova, S.S. Chesnokov, L.N. Kaptsov, A.V. Kudryashov, “Doughnut-like laser beam intensity output formation by means of adaptive optics”, Optics Express 155, pp.99-106, 1998.
- T.Yu. Cherezova, L.N. Kaptsov, A.V. Kudryashov, “CW industrial rod YAG:Nd3+ laser with an intracavity active bimorph mirror”, Applied Optics 35, pp.2554-2561, 1996.
- A.V. Kudryashov, V.I. Shmalhausen, “Semipassive bimproph flexible mirrors for atmospheric adaptive optics applications”, Optical Engineering 35(11), pp.3064-3073, 1996.
- T.Yu. Cherezova, S.S. Chesnokov, L.N. Kaptsov, A.V. Kudryashov, “Super-Gaussian output laser beam formation by bimorph adaptive mirror”, Optics Communications 155, pp.99-106, 1998.
- Test method for laser beam parameters: Beam width, divergence angle and beam propagation factor, Document ISO/DIS 11146, International Organization for Standardization, 1996.
- P. Belanger, Y. Champagne, C. Pare, “Beam propagation factor of diffracted laser beams”, Optic Communications 105, pp.233-242, 1994.
- T. Jonston, “Beam propagation (M2) measurement made as easy as it gets: the four-cuts method”, Applied Optics 37(21), July 1998.
- A.E. Siegman, Solid State Lasers: New Developments and Applications, pp.13-28, Plenum Press, New York, 1993.
- K. Roundy, “Propagation factor quantifies laser beam performance”, Laser Focus World 12, pp.119-122, 1999.
Return to Night N (opt) Ltd Scientific Activity page



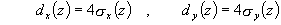 , (1)
, (1)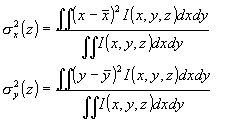 , (2)
, (2)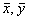 are the first moments of the intensity distribution
giving coordinates of the beam centre:
are the first moments of the intensity distribution
giving coordinates of the beam centre: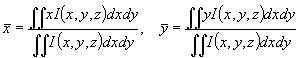 . (3)
. (3)

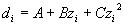 , (4)
, (4)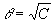 , (5)
, (5)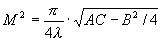 . (6)
. (6)
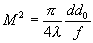 , (7)
, (7)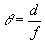 . (8)
. (8)
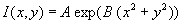 , (9)
, (9)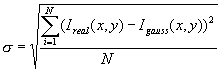 . (10)
. (10)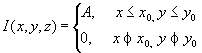 , (11)
, (11)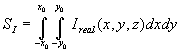 ) and
flat-top one (
) and
flat-top one (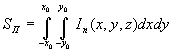 ):
):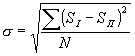 . (12)
. (12)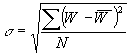 , (13)
, (13) is the averaged power of all frames measured per short time, N is the number of frames.
is the averaged power of all frames measured per short time, N is the number of frames.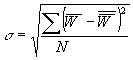 , (14)
, (14) is the averaged one measured for the compatible long time, N is
the number of counts of
is the averaged one measured for the compatible long time, N is
the number of counts of 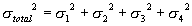 . (15)
. (15)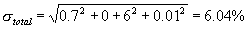 .
.